- HOME >
- ブログ
<<次の記事 前の記事>>
あとは学年順位発表を待つのみです。
さて、江南北校のエリアのある学校の中１でこんな問題が出ました。
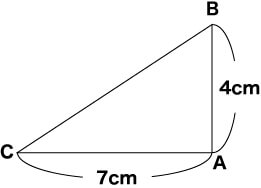
AB＝４ AC＝７の直角三角形ABCについてABを回転の軸として、１回転させてできる立体をP,ACを回転の軸としてできる立体をQとするとき、Pの体積はQの体積の何倍か？
計算終わりました？
フツーはPの体積は7×7×π×4×1/3だから、えっと・・・
ってなるよね。だから数学がキライとかって言いだす子がいそう。。。
計算がしんどいなーって思ったら、それは「数学」ではなくて「算数」！
4ｃｍと7ｃｍをそれぞれaとbに置き換えて考えてみよう
Ｐは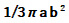
となり、 Ｑは
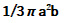となるね。
ここでＰ÷Ｑをすると・・・約分ができまくって・・・・
b/aとなるね。
だから答えは7/4倍になるんですね。
このＰはＱの何倍か・・・問題はよく出る！というかお約束パターンの問題！
つまり Ｑの軸の長さ÷Ｐの軸の長さ で答えが出るってことを経験で知っていると
めっちゃ簡単に解けるね。
螢雪ゼミナール江南北校では、宮田中 北部中 古知野中学の生徒を中心に
「数学の素晴らしさ」を教えています。
もっと数学が好きになりたい！苦手な数学を克服したい！って人は体験に是非きてくださいね。
期末テストが終わって
江南北校 鈴木 学
いよいよ学年末テスト（期末テスト）が終わって、点数が返ってきましたね。あとは学年順位発表を待つのみです。
さて、江南北校のエリアのある学校の中１でこんな問題が出ました。
AB＝４ AC＝７の直角三角形ABCについてABを回転の軸として、１回転させてできる立体をP,ACを回転の軸としてできる立体をQとするとき、Pの体積はQの体積の何倍か？
計算終わりました？
フツーはPの体積は7×7×π×4×1/3だから、えっと・・・
ってなるよね。だから数学がキライとかって言いだす子がいそう。。。
計算がしんどいなーって思ったら、それは「数学」ではなくて「算数」！
4ｃｍと7ｃｍをそれぞれaとbに置き換えて考えてみよう
Ｐは
となり、 Ｑはとなるね。ここでＰ÷Ｑをすると・・・約分ができまくって・・・・
b/aとなるね。
だから答えは7/4倍になるんですね。
このＰはＱの何倍か・・・問題はよく出る！というかお約束パターンの問題！
つまり Ｑの軸の長さ÷Ｐの軸の長さ で答えが出るってことを経験で知っていると
めっちゃ簡単に解けるね。
螢雪ゼミナール江南北校では、宮田中 北部中 古知野中学の生徒を中心に
「数学の素晴らしさ」を教えています。
もっと数学が好きになりたい！苦手な数学を克服したい！って人は体験に是非きてくださいね。
ケイセツゼミナール at 2021.2.26 15:13│comments (0)│trackback (x)│
|
コメント
コメントする
|
最近のエントリー
最近のコメント
- GPT-4
- この時期は、これ？
カテゴリー
- 鵜沼各務原校 (12件)
- 蘇原エール校 (113件)
- 那加校(小中学部) (29件)
- 長森校 (109件)
- 岐南校 (22件)
- 陽南本荘校 (17件)
- 則武校(小中学部） (18件)
- 柳津校 (43件)
- 北方真正校 (23件)
- 瑞穂校 (3件)
- 鏡島校 (19件)
- 大垣北校 (6件)
- 安井校 (36件)
- 安八校 (12件)
- 大野校 (14件)
- 平田校 (9件)
- 池田校 (9件)
- 江南北校 (29件)
- 扶桑校 (11件)
- 布袋校 (11件)
- 稲沢校 (22件)
- 一宮開明校 (11件)
- 木曽川校 (7件)
- 如意申校 (9件)
- 鳴海校 (2件)
- 岐阜駅前校（高校部) (4件)
- 那加校(高校部) (7件)
- 則武校（高校部） (7件)
- 教育本部センター (2件)
- 鏡島校（螢雪パーソナル） (4件)
- 那加校（螢雪パーソナル） (4件)
- 当知校（螢雪パーソナル） (12件)